昨天我們繼續看了 Multiple Features 的 Linear Regression，接下來讓我們來看看 Classification 吧！

Classification 也就是分類問題，像是幫郵件標記是否為垃圾郵件、判別是否患病、判斷圖片中的動物是哪一種等等。這些問題都屬於分類問題，目標是依據現有的資訊推斷分在哪些有限類別當中是合理的。

Logistic Regression

在還沒進入到 Neural Network 之前，我們這裡談的 Classification 作法都僅限於以 Logistic Regression。

Logistic Regression 是一種二元分類器，一個資料不是被分在 A 就是分在 B。

它的概念也十分簡單，就是透過一條線去隔開兩個區域，落在區域 A 的分做一類；落在區域 B 的分做另一類。
底下的圖是一個例子，在直線上方的資料會被預測為綠色，在直線之下則被預測為紅色。

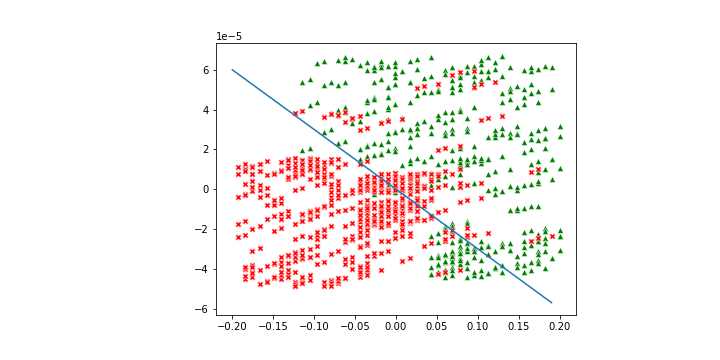
依照過去的經驗我們知道，要訓練一個模型會需要

1. 定義函數
2. 將資料輸入進模型，並評估模型好壞
3. 調整參數大小

我們就一步一步來看 Logistic Regression 會如何處理吧！

模型設定

在 Logistic Regression 我們會做出一個模型 ，並且保證 。你可以把它當成是一個機率模型，如果機率大於 ，就預測為 A 類，否則是 B 類。

這時候的 經常會套用如 Sigmoid 這類的函數，因為它是可微函數，又能符合剛剛的條件。你可能也會聽過 ReLU ，不過這裡我們先以 Sigmoid 來說明。

Sigmoid 函數原先的定義如下。

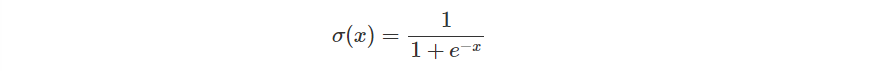
在 Logistic Regression 定義的 定義則是如下。

評估模型

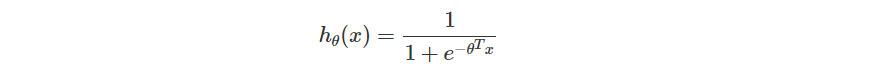
現在我們已經定義好函數了，那下一個問題自然是要如何評估一個模型的好壞了。
要讓模型表現越好，意味著預測正確的次數需要比較多。

• 如果今天答案是 False，卻預估成比較大的 True，那應該要讓數字更新得更小。
• 如果今天答案是 True，卻預估成比較小的 False，那應該要讓數字更新得更大。

所以我們設定了這樣的單一 Loss Function。

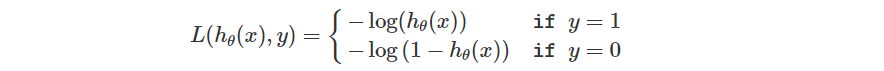
觀察一下 Loss Function，其實這個敘述跟前面是相同的。
底下是兩個 log 函數的圖形可以參考。

• 當答案是 True，如果 越小，那誤差也就越大
• 當答案是 False，如果 越大，那誤差也就越大

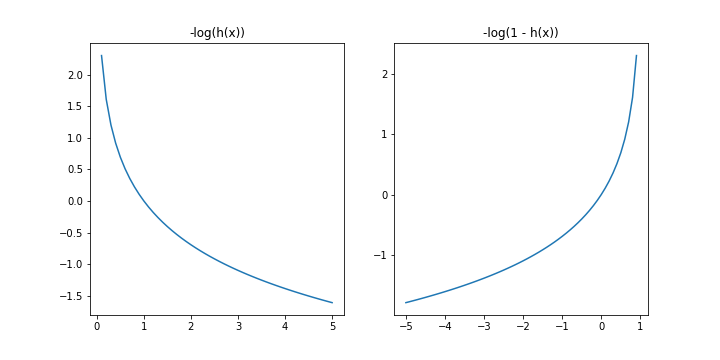
不過把一個函數寫成兩個 Case 可能不是那麼好看，所以更多時候我們會進一步把函數用底下這個方法來描述他。

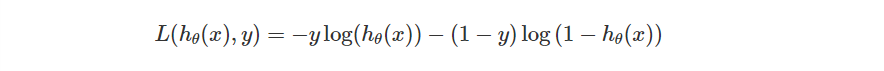
不過這只是單一資料的 Loss，整體的誤差同樣會有一個總和取平均。

調整模型參數

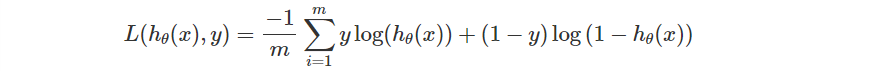
最後一步自然就會是調整模型參數了。我們同樣可以採取 Gradient Descent。這意味著我們會需要在 Loss Function 對每個參數 偏微分，然後更新參數。

首先稍微整理一下 Loss Function 吧！

避免忘記定義

第三個等號如果想不出來的話可以參考

接下來推導偏微分

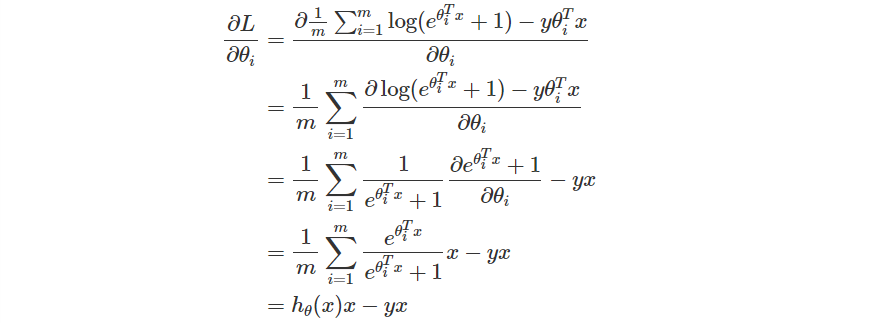
偏微分推導出來之後，接下來就是跟過去一樣，設定一個 Learning Rate，然後把每一個參數乘上梯度後往負方向更新。

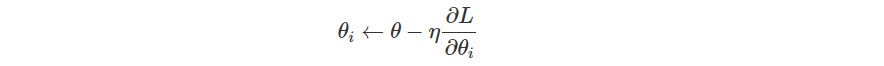
推導的部分還沒跟上沒關係，只要大概念懂了，這邊再慢慢補回來就好！

小結

今天我們看到新的機器學習問題 Classification。對於簡單的二元分類問題我們可以直接使用 Logistic Regression 解決。
做法是透過訓練一個函數，如果資料落在函數隔出的區域 A 就分成一類，落在另一區 B 的分成一類。

步驟上我們都還是照著過去的步驟，先定義模型、設定評估模型的函數，最後去調整模型參數。

不過這裡同樣的，我們直接告訴你要怎麼設計模型、如何設定 Loss，但這部分如果做修改的話還是會有不同的效果出現。只不過這邊提及的設定方式比較常見，因此這邊就單純介紹這個部分。

明天我們會從 Kaggle 取得資料，實際來試試看 Logistic Regression 實作起來跟 Linear Regression 有哪些異同。